This problem is a programming version of Problem 189 from projecteuler.net
Consider the following configuration of triangles:
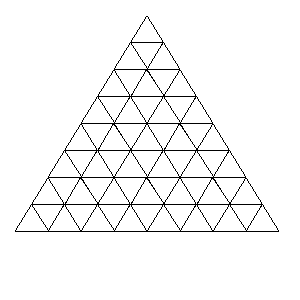
We wish to colour the interior of each triangle with one of three colours: red, green or blue, so that no two neighbouring triangles have the same colour. Such a colouring shall be called valid. Here, two triangles are said to be neighbouring if they share an edge.
Note: if they only share a vertex, then they are not neighbours.
For example, here is a valid colouring of the above grid:
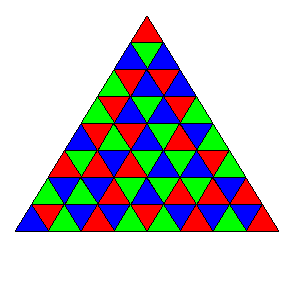
A colouring which is obtained from a colouring by rotation or reflection is considered from unless the two are identical.
Let's assume we have colours and triangles formed into above configuration. How many distinct valid colourings are there for such configuration?
Input Format
The only line of the test contains two integers: and .
Constraints
Output Format
Print exactly one integer which is the answer to the problem. Since that number could be very large, output it modulo .
Sample Input 0
1 3
Sample Output 0
3
Explanation 0
We can colour the only triangle in each of the three given colours.