_{This problem is a programming version of Problem 143 from projecteuler.net}

Let be a triangle with all interior angles being less than degrees. Let be any point inside the triangle and let , , and .

Fermat challenged Torricelli to find the position of such that was minimised.

Torricelli was able to prove that if equilateral triangles , and are constructed on each side of triangle , the circumscribed circles of , , and will intersect at a single point, , inside the triangle. Moreover he proved that , called the Torricelli/Fermat point, minimises . Even more remarkable, it can be shown that when the sum is minimised, and that , and also intersect at .

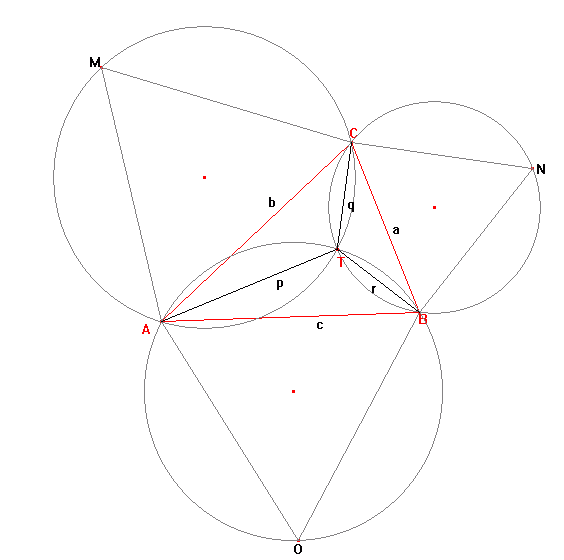
If the sum is minimised and , , , , and are all positive integers we shall call triangle a Torricelli triangle. For example, , , is an example of a Torricelli triangle, with .

Given , print all the side lengths of all Torricelli triangles having . To ensure that no triangle is printed more than once, ensure that . Print the triangles with smaller first, and in case of ties, smaller s, and in case of ties, smaller s.