This problem is a programming version of Problem 107 from projecteuler.net
The following undirected network consists of seven vertices and twelve edges with a total weight of .
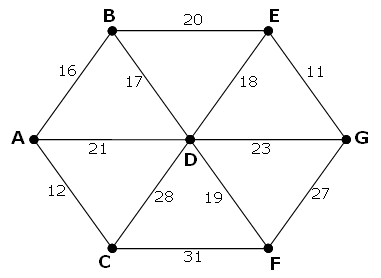
The same network can be represented by the matrix below.

However, it is possible to optimise the network by removing some edges and still ensure that all points on the network remain connected. The network which achieves the maximum saving is shown below. It has a weight of , representing a saving of from the original network.
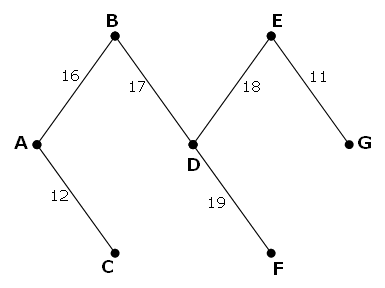
containing a network with forty vertices, and given in matrix form, find the maximum saving which can be achieved by removing redundant edges whilst ensuring that the network remains connected.
Input Format
First line contains two integers (Number of nodes) and (Number of edges) separated by a space.
Next lines contains 3 integers and representing an undirected edge betwen and who's weght is .
Constraints
If there are edges between the same pair of nodes with different weights, they are to be considered as is, like multiple edges.
Output Format
Print the total weight of the resulting graph.
Sample Input
7 12
1 2 16
1 3 12
1 4 21
2 4 17
2 5 20
3 4 28
3 6 31
4 5 18
4 6 19
4 7 23
5 7 11
6 7 27
Sample Output
93