A spider, S, sits in one corner of a cuboid room, measuring 6 by 5 by 3, and a fly, F, sits in the opposite corner. By travelling on the surfaces of the room the shortest "straight line" distance from S to F is 10 and the path is shown on the diagram.
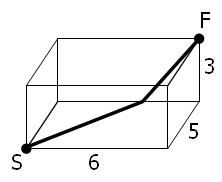
However, there are up to three "shortest" path candidates for any given cuboid and the shortest route doesn't always have integer length.
By considering all cuboid rooms with integer dimensions, up to a maximum size of by by , there are exactly 2060 cuboids for which the shortest route has integer length when M=100; the number of solutions is 1975 when M=99.
There would be testcases , For each case , an integer would be given . For each case, print the number of cuboids with integer dimensions up to a maximum of by by such that the shortest route is an integer.
An by by dimension cuboid is upto a maximum of by by only if
, , .
Input Format
First line contains denoting the number of testcases. Next lines contain an integer .
Constraints
Output Format
lines each containing the answer for that case.
Sample Input
2
99
100
Sample Output
1975
2060