BATIBots

The year is 3000. Brainy Automated Transcendental Intelligent Bots (BATIBot for short) guard Mactan from colonizers.
Each BATIbot has a starting life number, a positive integer greater than or equal to 1. Starting life numbers of two different BATIbots may be the same. The life number of a BATIbot may be modified if they get attacked by evil bots.
Magell-1 wants to terrorize Mactan by sending an army of evil robots. They come in two types:
A Primebot is an evil bot whose damage number is some prime number . If it attacks a BATIbot whose current life number is NOT divisible by , nothing happens. Otherwise, the BATIbot's current life number is divided by . If the new life number is NOT divisible by after the attack, the BATIbot immediately dies. A Primebot immediately dies after attacking.
A Lubot is an evil bot whose damage number is a positive integer . If it attacks a BATIbot whose current life number is NOT divisible by , nothing happens. If it attacks a BATIbot whose starting life number is , nothing happens. Else, the BATIbot's current life number is divided by . If the new life number is , the BATIbot dies.
A BATIbot is said to be strong if it is guaranteed to survive ONE attack of any Primebot or ANY NUMBER of attacks of any single Lubot.
Here are some examples:
A BATIbot with starting life number cannot be killed by a Lubot whose damage number is . However, it can be killed by a Primebot whose damage number is . Therefore, such a BATIbot is NOT strong.
A BATIbot with starting life number can be killed by two attacks of a Lubot with damage number . Therefore, such a BATIbot is NOT strong.
A BATIbot with starting life number can be killed by a single attack of a Primebot whose damage number is . Therefore, such a BATIbot is NOT strong.
One can verify that a BATIbot with starting life number is strong.
Let us model the city of Mactan as a grid drawn on the Cartesian plane with corners , , , and . We denote by the cell which has four corners , , and . Cell has exactly one BATIbot with starting life number .
A barangay of Mactan is defined as a rectangular subgrid of the original grid. A barangay can then be represented by a pair of lattice points with and . With this representation, we can deduce that:
- it has four corners , , , and .
- the territory of the barangay is the set of cells such that and .
The boundary of barangay is defined as the set of points contained in any of its four sides, including the corners.
A barangay is said to be protected if it contains exactly one strong BATIbot.
A partition of Mactan into barangays is valid if and only if:
Each cell belongs to exactly one barangay.
No point is contained in the boundaries of exactly three barangays. It can be less than or greater than three.
For example, the following partition (into four barangays) is not valid:
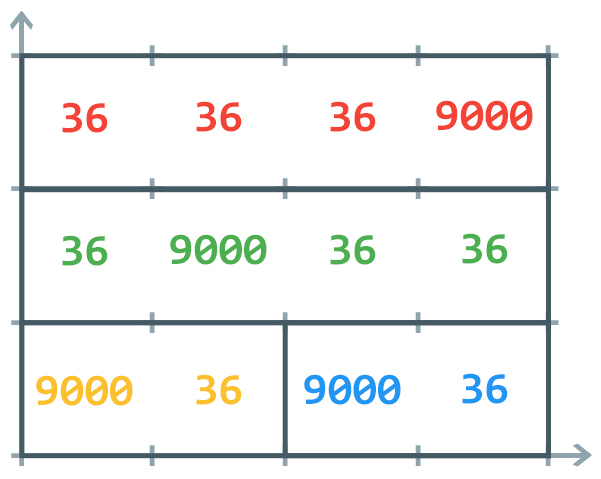
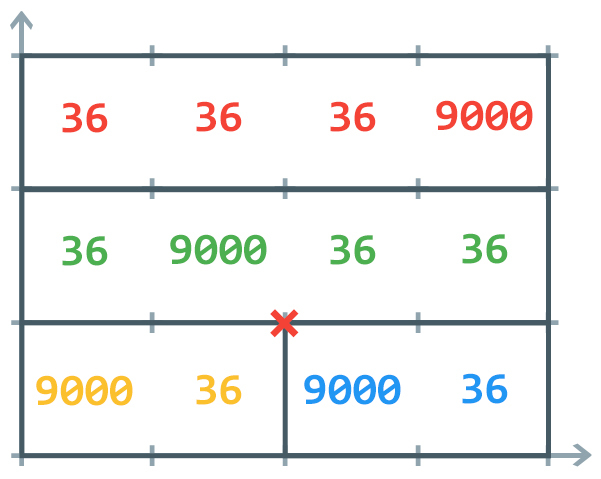
This is not a valid partition because although every cell is in exactly one barangay, the point is in the boundaries of exactly three barangays:
- .
- .
- .
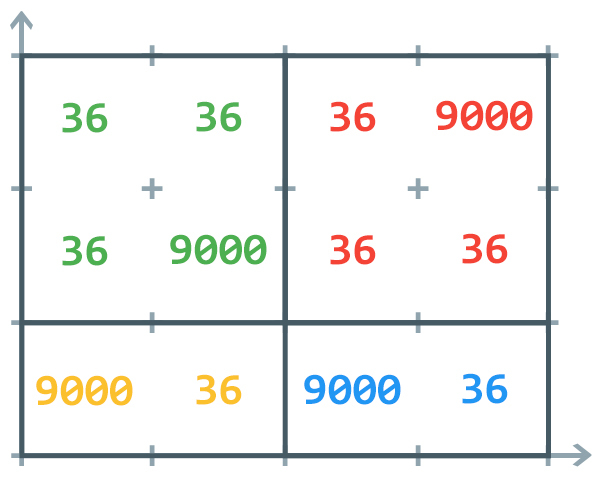
On the other hand, you can verify that the following partition is valid:
Your task, assigned by Mayor Lapu-2, is to figure out how many ways one can validly partition Mactan into protected barangays. You decide how many barangays there are in the partition, as long as all of them turn out to be protected.
Input Format
The first line of input contains , the number of test cases.
The first line of each test case contains two space-separated integers and . The next lines contains numbers each, and together, they describe the grid in the following format:
In other words, is the th number in the th line.
Constraints
The sum of all in a single file is .
Subtask 1 (17 points):
Subtask 2 (15 points):
Subtask 3 (18 points):
Subtask 4 (18 points):
Subtask 5 (12 points):
Subtask 6 (20 points):
No additional constraints.
Output Format
For each test case, output a single line containing a single integer denoting the answer modulo .
Sample Input 0
1
3 4
36 36 36 9000
36 9000 36 36
9000 36 9000 36
Sample Output 0
2
Explanation 0
There are two valid partitions:
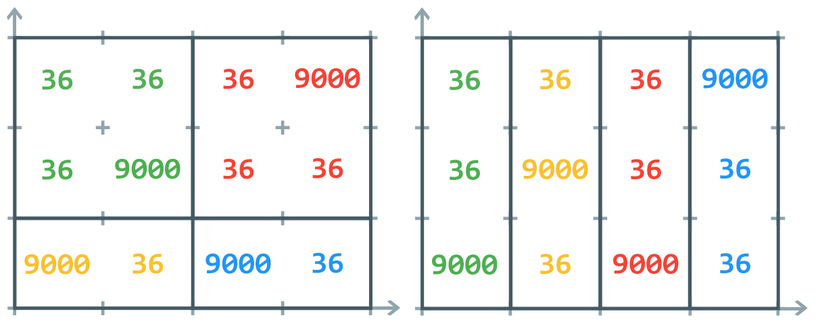
Thus, we output modulo which is just .
xxxxxxxxxxusing namespace std;int main() { /* Enter your code here. Read input from STDIN. Print output to STDOUT */ return 0;}