We use cookies to ensure you have the best browsing experience on our website. Please read our cookie policy for more information about how we use cookies.
  1. Prepare
  2. Mathematics
  3. Combinatorics
  4. Robanukkah Tree

Robanukkah Tree

Robot Bender is celebrating Robanukkah, the most important holiday for robots.

He stole bought a Robanukkah tree, which is actually a common tree (i.e., a connected acyclic graph with vertices). He wants to decorate it with regular polyhedrons by placing one regular polyhedron in each vertex.

A regular polyhedron is a convex polyhedron whose faces are identical regular polygons. There are five types of regular polyhedrons:

Bender has types of polyhedrons. All polyhedrons of the same type are indistinguishable by their shape. Bender has at least polyhedrons of each available type.

In addition, Bender has colors. He paints each face of each polyhedron in one of these colors.

Bender considers two polyhedrons to be similar if one of the following is true:

  • They are of the same type.
  • Some face of the first polyhedron and some face of the second polyhedron are painted with the same color.

Bender considers the decorated tree to be beautiful if any two adjacent vertices don't contain similar polyhedrons. In particular, any decoration of a one-vertex tree is beautiful.

Two polyhedrons are equally painted if it is possible to rotate and move one of them so that it coincides with the other and the coincided faces are painted in the same color.

Two decorations of the tree are the same if each vertex in both decorations has equally painted polyhedrons.

Can you help Bender find the number of ways he can decorate his tree beautifully? Find and print it modulo .

Input Format

The first line contains three space-separated integers denoting the respective values of (the number of vertices in the tree), (the number of available colors), and (the number of types of polyhedrons).
The second line contains different space-separated numbers describing , where is the number of faces of polyhedrons of the type. .
The third line contains space-separated numbers describing , where is index of parent of vertex. The root of the tree has index .

Note: If the tree consists of only one vertex, the third line will be empty.

Constraints

Output Format

Print a single integer denoting the number of ways to decorate the tree modulo .

Sample Input

3 3 2
4 6
1 1

Sample Output

408

Explanation

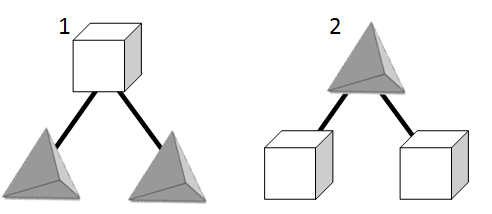
Let's consider all ways to decorate the given Robanukkah tree:

  1. Cube in the root, tetrahedrons in the leaves.
    • All faces of the cube are painted in the same color (which can be chosen in ways). Each tetrahedron can then be independently painted using one or two of the remaining colors, and there are ways to do this. In total, there are ways.
    • Faces of the cube are painted in exactly two colors (the pair of colors can be chosen in ways). There are ways to paint a cube using exactly two colors. The painting of tetrahedrons will be clearly defined: all faces of both of them should be painted in the leftover color. In total, ways.
  2. Tetrahedron in the root, cubes in the leaves.
    • All faces of the tetrahedron are painted in the same color (which can be chosen in ways). Each cube can then be independently painted using one or two of the remaining colors, and there are ways to do that. In total, ways.
    • Faces of the tetrahedron are painted in exactly two colors (which can be chosen in ways). There are ways to paint the tetrahedron in exactly two colors. The painting of each cube will be clearly defined in that all faces of both of them should be painted in the leftover color. In total, ways.

In total, .

Note: Your output must be modulo .