We use cookies to ensure you have the best browsing experience on our website. Please read our cookie policy for more information about how we use cookies.
  1. Prepare
  2. Algorithms
  3. Dynamic Programming
  4. HackerRank City
  5. Discussions

HackerRank City

Sort by

recency

|

41 Discussions

|

  • Tusenka
     + 0 comments

    Why there is the (Z+a*2)*Y from sum for X=X*4+(Z+a*2)*Y+(Z+a*3)*Y*2+Z*2+a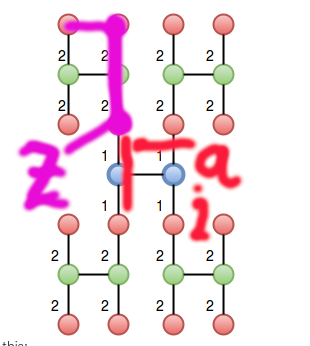

  • Tusenka
     + 0 comments

    Why there is the (Z+a*2)*Y form sum for X=X*4+(Z+a*2)*Y+(Z+a*3)*Y*2+Z*2+a What does it mean?

  • Tusenka
     + 0 comments

    Why the solution from aditorial doesn't work https://codefile.io/f/dLpV7c5XBt

  • Tusenka
     + 0 comments

    From editorial why 8? I don't quite understande te editorial solution. Could anyone explain me those forumulas more deeply?

  • apkworldsites77
     + 0 comments

    Coding for hours can make anyone hungry! In Singapore, we have so many tasty options, from hawker food to quick snacks. If you ever need a fun treat while working, the Golden Village popcorn menu has some great choices—like their caramel popcorn, which is perfect for a late-night coding session.