You are an elemental sorcerer who owns a shop that sells magical orbs, with each orb containing the power of some distinct element (e.g., Fire, Water, Earth, etc.). The shop has a shelf with horizontal slots, where each slot has the capability of holding exactly orb.
Being a novice sorcerer, your elemental knowledge is just , i.e. you know only different kinds of elemental spells, where each can conjure identical orbs of a distinct element type. Before the shop opens next morning, you want to fill all the shelf with such orbs; no slot should remain unoccupied.
Now, to fill the shelf, you conjure orbs of up to different types (or elements) and arrange it on the shelf. However, each element has a blasting threshold, , meaning that if there are more than contiguously-placed orbs of element type placed anywhere on the shelf, they will explode and destroy the shelf and the orbs in it. The shelf may contain less than distinct types of orbs as long as the configuration will not explode.
You want to find the number of possible configurations to arrange the shelf with these elemental orbs without any explosion.
You are given the values of , , and the blasting threshold for each element . Find and print the number of distinct ways, modulo , on a new line.
Note: All orbs of the same element type are identical, but each slot in a shelf is distinct. You can conjure any type of orb an infinite number of times.
Input Format
The first line contains an integer, , number of test cases. The subsequent lines describe each tescase over two lines:
- The first line of each test case contains two space-separated integers describing the respective values of (the shelf's capacity) and (elemental knowledge).
- The second line of each test case contains space-separated integers describing (i.e., the respective blasting thresholds for all elements).
Constraints
Output Format
For each test case, print an integer on a new line describing the number of distinct ways to arrange orbs on the shelf, modulo .
Sample Input 0
2
5 2
1 1
5 2
5 5
Sample Output 0
2
32
Explanation 0
The diagram below depicts the possible valid and invalid configurations for the first shelf, described as , , and :
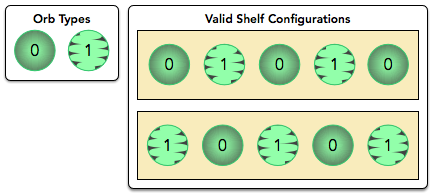
Because the blasting threshold for both types of orbs is , any configuration containing more than consecutive orb of the same type will cause the shelf to explode. As there are only two valid configurations for this shelf, we print the result of on a new line.