We use cookies to ensure you have the best browsing experience on our website. Please read our cookie policy for more information about how we use cookies.
  1. Prepare
  2. Algorithms
  3. Graph Theory
  4. Breadth First Search: Shortest Reach

Breadth First Search: Shortest Reach

Consider an undirected graph where each edge weighs 6 units. Each of the nodes is labeled consecutively from 1 to n.

You will be given a number of queries. For each query, you will be given a list of edges describing an undirected graph. After you create a representation of the graph, you must determine and report the shortest distance to each of the other nodes from a given starting position using the breadth-first search algorithm (BFS). Return an array of distances from the start node in node number order. If a node is unreachable, return for that node.

Example
The following graph is based on the listed inputs:

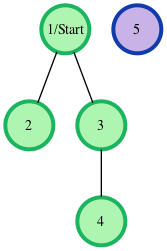
image

// number of nodes
// number of edges

// starting node

All distances are from the start node . Outputs are calculated for distances to nodes through : . Each edge is units, and the unreachable node has the required return distance of .

Function Description

Complete the bfs function in the editor below. If a node is unreachable, its distance is .

bfs has the following parameter(s):

  • int n: the number of nodes
  • int m: the number of edges
  • int edges[m][2]: start and end nodes for edges
  • int s: the node to start traversals from

Returns
int[n-1]: the distances to nodes in increasing node number order, not including the start node (-1 if a node is not reachable)

Input Format

The first line contains an integer , the number of queries. Each of the following sets of lines has the following format:

  • The first line contains two space-separated integers and , the number of nodes and edges in the graph.
  • Each line of the subsequent lines contains two space-separated integers, and , that describe an edge between nodes and .
  • The last line contains a single integer, , the node number to start from.

Constraints

Sample Input

2
4 2
1 2
1 3
1
3 1
2 3
2

Sample Output

6 6 -1
-1 6

Explanation

We perform the following two queries:

  1. The given graph can be represented as:
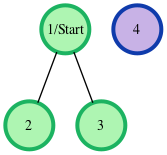
    image
    where our start node, , is node . The shortest distances from to the other nodes are one edge to node , one edge to node , and an infinite distance to node (which it is not connected to). We then return an array of distances from node to nodes , , and (respectively): .

  2. The given graph can be represented as:
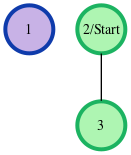
    image
    where our start node, , is node . There is only one edge here, so node is unreachable from node and node has one edge connecting it to node . We then return an array of distances from node to nodes , and (respectively): .

Note: Recall that the actual length of each edge is , and we return as the distance to any node that is unreachable from .