This problem is a programming version of Problem 147 from projecteuler.net
In a 3x2 cross-hatched grid, a total of 37 different rectangles could be situated within that grid as indicated in the sketch.
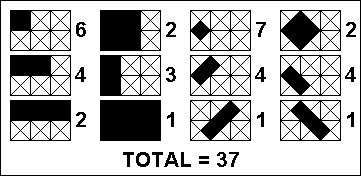
There are 5 grids smaller than 3x2, vertical and horizontal dimensions being important, i.e. 1x1, 2x1, 3x1, 1x2 and 2x2. If each of them is cross-hatched, the following number of different rectangles could be situated within those smaller grids:
1x1: 1
2x1: 4
3x1: 8
1x2: 4
2x2: 18
Adding those to the 37 of the 3x2 grid, a total of 72 different rectangles could be situated within 3x2 and smaller grids.
How many different rectangles could be situated within and smaller grids? To make the task more challenging, you need to output the number of upright and diagonal rectangles separately.
Since the numbers can be large, output them modulo .
Input Format
The first line of input contains , the number of test cases.
Each test case consists of one line containing two integers, and , separated by a space.
Constraints
In test file #1:
In test file #2:
In test file #3:
In test file #4:
Output Format
For each test case, output a single line containing two integers separated by single spaces:
- The number of upright rectangles.
- The number of diagonal rectangles.
Sample Input
1
3 2
Sample Output
40 32
Explanation
Of the rectangles that could be situated within and smaller grids, of those are upright and are diagonal.