This problem is a programming version of Problem 126 from projecteuler.net
The minimum number of cubes to cover every visible face on a cuboid measuring is twenty-two.
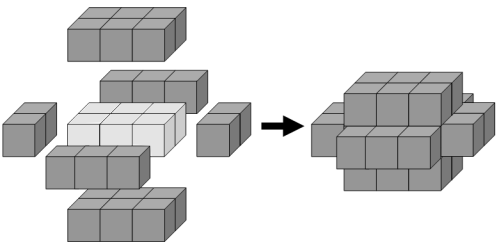
If we then add a second layer to this solid it would require forty-six cubes to cover every visible face, the third layer would require seventy-eight cubes, and the fourth layer would require one-hundred and eighteen cubes to cover every visible face.
However, the first layer on a cuboid measuring also requires twenty-two cubes; similarly the first layer on cuboids measuring , , and all contain forty-six cubes.
We shall define to represent the number of cuboids that contain cubes in one of its layers. So , , , and .
Given , compute .
Input Format
The first line of input contains , the number of test cases. Each test case consists of a single line containing a single integer, .
Constraints
For the first few test files worth 25% of the total points:
For the next few test files worth 25% of the total points:
For the last few test files worth 50% of the total points:
Output Format
For each test case, output a single line containing a single integer, the value .
Sample Input
5
22
46
78
118
154
Sample Output
2
4
5
8
10
Explanation
The sample I/O are mentioned in the problem statement.