_{This problem is a programming version of Problem 109 from projecteuler.net}

In the game of darts a player throws three darts at a target board which is split into twenty equal sized sections numbered one to twenty.

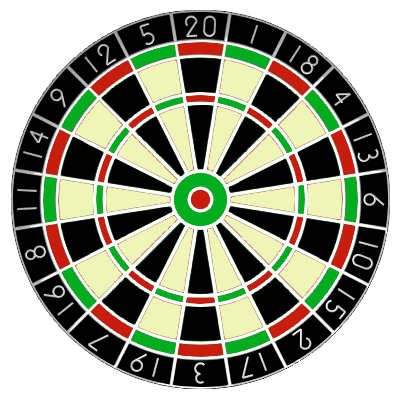
The score of a dart is determined by the number of the region that the dart lands in. A dart landing outside the red/green outer ring scores zero. The black and cream regions inside this ring represent single scores. However, the red/green outer ring and middle ring score double and treble scores respectively.

At the centre of the board are two concentric circles called the bull region, or bulls-eye. The outer bull is worth points and the inner bull is a double, worth points.

There are many variations of rules but in the most popular game the players will begin with a score or and the first player to reduce their running total to zero is a winner. However, it is normal to play a "doubles out" system, which means that the player must land a double (including the double bulls-eye at the centre of the board) on their final dart to win; any other dart that would reduce their running total to one or lower means the score for that set of three darts is "bust".

When a player is able to finish on their current score it is called a "checkout" and the highest checkout is (two treble 20s and double bull).

There are exactly 14 distinct ways to checkout on a score of :

Note that is considered different to as they finish on different doubles. Moreover, the combination is also considered different to .

In addition we shall not include misses in considering combinations; for example, is the same as and .

Now imagine you have an infinite number of darts. Now you can stop on every double you get. How many ways you have to checkout with score ?