Simon received the board game Ticket to Ride as a birthday present. After playing it with his friends, he decides to come up with a strategy for the game.
There are cities on the map and road plans. Each road plan consists of the following:
- Two cities which can be directly connected by a road.
- The length of the proposed road.
The entire road plan is designed in such a way that if one builds all the roads, it will be possible to travel between any pair of cities.
A ticket enables you to travel between two different cities. There are tickets, and each ticket has a cost associated with it. A ticket is considered to be useful if there is a path between those cities.
Simon wants to choose two cities, and , and build a minimal number of roads so that they form a simple path between them. Let be the sum of costs of all useful tickets and be the sum of lengths of all the roads Simon builds. The profit for pair is defined as . Note that and are not necessarily unique and may be the same cities.
Given road plans and ticket prices, help Simon by printing the value of his maximum possible profit on a new line.
Input Format
The first line contains single positive integer, , denoting the number of cities.
Each of the subsequent lines contains three space-separated integers describing the respective values of , , and for a road plan, where , , and . Here, and are two cities that the road plan proposes to connect and is the length of the proposed road.
The next line contains a single positive integer, , denoting the number of tickets.
Each of the subsequent lines contains three space-separated integers describing the respective values of , , and for a ticket from city to city (where is the cost of the ticket).
Constraints
Output Format
Print a single integer denoting the the maximum profit Simon can make.
Time Limits
- seconds for Java and C#.
- Please refer to our Environment page to see time limits for other languages.
Sample Input
7
1 2 1
1 3 1
1 4 4
4 5 1
4 6 1
4 7 1
5
5 7 3
3 6 2
3 4 10
2 7 15
1 6 7
Sample Output
13
Explanation
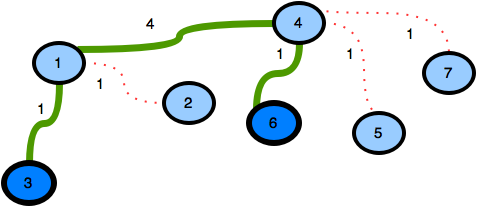
Simon can maximize his profit by choosing the pair .
The roads on the path between them are , , and . The total road length is .
The useful tickets are , , and . The total ticket cost is .
The profit is .