Treeland is a country with cities and roads. There is exactly one path between any two cities.
The ruler of Treeland wants to implement a self-driving bus system and asks tree-loving Alex to plan the bus routes. Alex decides that each route must contain a subset of connected cities; a subset of cities is connected if the following two conditions are true:
- There is a path between every pair of cities which belongs to the subset.
- Every city in the path must belong to the subset.

In the figure above, is a connected subset, but is not (for the second condition to be true, would need to be part of the subset).
Each self-driving bus will operate within a connected segment of Treeland. A connected segment where is defined by the connected subset of cities .
In the figure above, is a connected segment that represents the subset . Note that a single city can be a segment too.
Help Alex to find number of connected segments in Treeland.
Input Format
The first line contains a single positive integer, . The subsequent lines each contain two positive space-separated integers, and , describe an edge connecting two nodes in tree .
Constraints
Subtasks
- For score:
- For score:
Output Format
Print a single integer: the number of segments , which are connected in tree .
Sample Input
3
1 3
3 2
Sample Output
5
Explanation
The connected segments for our test case are: , , , , and . These segments can be represented by the respective subsets: , , , , and .
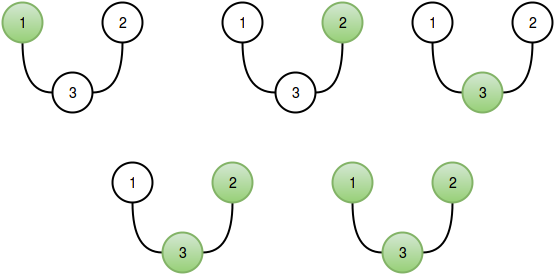
Note: is not a connected segment. It represents the subset and the path between and goes through which is not a member of the subset.