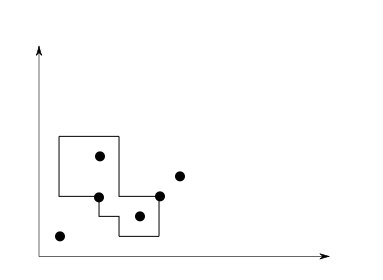
There are N points on X-Y plane with integer coordinates (xi, yi). You are given a set of polygons with all of its edges parallel to the axes (in other words, all angles of the polygons are 90 degree angles and all lines are in the cardinal directions. There are no diagonals). For each polygon your program should find the number of points lying inside it. A point located on the border of polygon is also considered to be inside the polygon.

Input Format
The first line contains two integers N and Q. The next line contains N space-separated integer coordinates (xi,yi). Q queries follow. Each query consists of a single integer Mi in the first line, followed by Mi space separated integer coordinates (x[i][j],y[i][j]) specifying the boundary of the query polygon in clock-wise order.

• Polygon is an alternating sequence of vertical line segments and horizontal line segments.
• Polygon has Mi edges, where (x[i][j],y[i][j]) is connected to (x[i][(j+1)%Mi], y[i][(j+1)%Mi].
• For each 0 <= j < Mi, either x[i][(j+1)%Mi] == x[i][j] or y[i][(j+1)%Mi] == y[i][j] but not both.
• It is guaranteed that the polygon is not self-intersecting.

Output Format
For each query output the number of points inside the query polygon in a separate line.

Constraints
1 <= N <= 20,000
1 <= Q <= 20,000
4 <= Mi <= 20
-200,000 <= x[i][j],y[i][j] <= 200,000

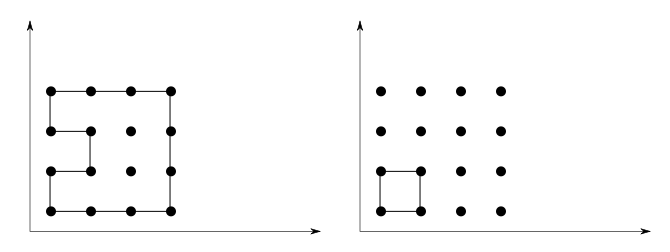
Sample Input #1
16 2
0 0
0 1
0 2
0 3
1 0
1 1
1 2
1 3
2 0
2 1
2 2
2 3
3 0
3 1
3 2
3 3
8
0 0
0 1
1 1
1 2
0 2
0 3
3 3
3 0
4
0 0
0 1
1 1
1 0

Sample Output #1:
16
4

Sample Input #2:
6 1
1 1
3 3
3 5
5 2
6 3
7 4
10
1 3
1 6
4 6
4 3
6 3
6 1
4 1
4 2
3 2
3 3

Sample Output #2:
4