You are given 2 integers a and b. Let a number be defined as 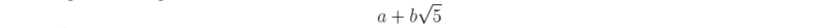. As we know 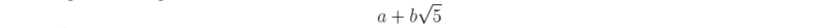will be an irrational number when b is non-zero. In this problem, we call it the AC number. We define

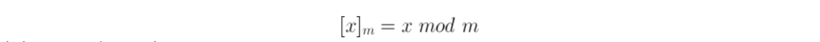(where x an integer)

and the operation on AC number as:

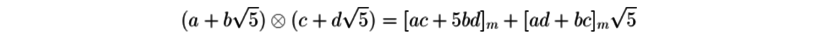
This problem is to find the smallest positive integer n, such that:

We call the integer n as period. You are given a, b and m. Can you figure out the period?

Input Format
The first line of the input contains a single integer T denoting the number of test-cases.
T lines follow, each containing 3 integers - a, b and m separated by a single space.

Output Format
Output the Period if it exists, otherwise output "-1" (quotes only for reference)

Constraints
1 ≤ T ≤ 300
5 ≤ m ≤ 10⁷
0 ≤ a, b < m

Sample Input #00

4
0 0 13
1 0 7
3 0 10007
1 1 19

Sample Output #00

-1
1
5003
18

Explanation #00

For the 1st test-case, no amount of operation ⊗ on a = 0, b = 0 gives 1 on the RHS. Hence the answer is -1.
When a = 1, b = 0, we have 1 for n = 1.
On repeated operations, the third and the fourth testcases sum to 1 for n = 5003 and n = 18 respectively.