John lives in HackerLand, a country with cities and bidirectional roads. Each of the roads has a distinct length, and each length is a power of two (i.e., raised to some exponent). It's possible for John to reach any city from any other city.
Given a map of HackerLand, can you help John determine the sum of the minimum distances between each pair of cities? Print your answer in binary representation.
Input Format
The first line contains two space-seperated integers denoting (the number of cities) and (the number of roads), respectively.
Each line of the subsequent lines contains the respective values of , , and as three space-separated integers. These values define a bidirectional road between cities and having length .
Constraints
- ,
- If , then .
Output Format
Find the sum of minimum distances of each pair of cities and print the answer in binary representation.
Sample Input
5 6
1 3 5
4 5 0
2 1 3
3 2 1
4 3 4
4 2 2
Sample Output
1000100
Explanation
In the sample, the country looks like this:
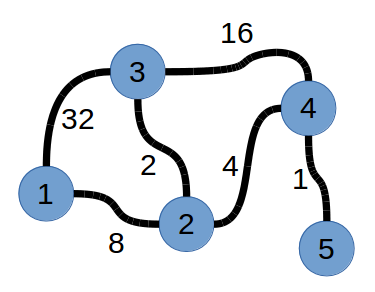
Let be the minimum distance between city and city .