There is an obstacle on a 2D plane in the form of a simple polygon with vertices at points . Vertex connects with vertex via a rope. Each point on the rope is outside the polygon, but the points can be on the boundary. The rope is elastic, meaning it always tries to minimize its length and the friction force between the obstacle and the rope is zero. The ends of the rope are fixed at points and and no other point on the rope is fixed.
If the shape of the rope is a line that has never intersects with or overlaps itself, what's the maximum possible length of the rope?
Input Format
The first line contains three space-separated integers describing the respective values of , , and .
Each line of the subsequent lines contains two space-separated integers denoting the respective values of and corresponding to the polygon's vertices in clockwise or counterclockwise order.
Constraints
- It's guaranteed that the input polygon is simple.
Output Format
Print a single floating-point number denoting the maximum possible length of the rope. The answer is considered to be correct if it has an absolute error of at most .
Sample Input 0
4 2 4
100 100
200 100
200 200
100 200
Sample Output 0
200
Explanation 0
In the diagram below, the red line depicts the rope:

Sample Input 1
6 4 1
167 84
421 84
283 192
433 298
164 275
320 133
Sample Output 1
468.3361845326
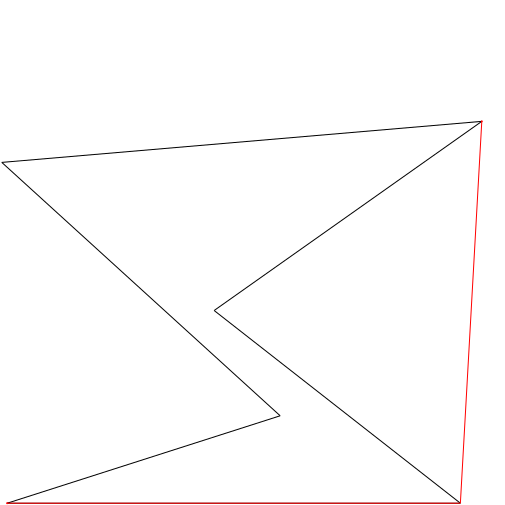
Explanation 1
In the diagram below, the red line depicts the rope: