You are given a N * N matrix, U. You have to choose 2 sub-matrices A and B made of only 1s of U, such that, they have at least 1 cell in common, and each matrix is not completely engulfed by the other, i.e.,

If U is of the form

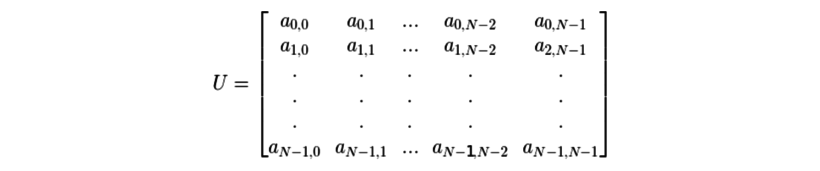
and A is of the form

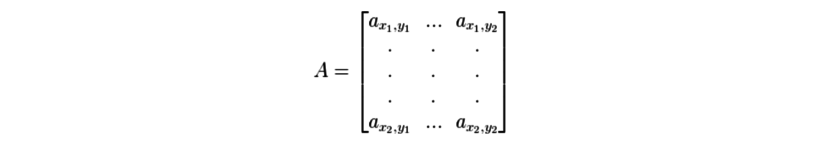
and B is of the form

then, there exists atleast 1 a_{i, j} : a_{i, j} ∈ A and a_i,j ∈ B
then, there exists atleast 1 a_{i1, j1} : a_{i1, j1} ∈ A and a_i1,j1 ∉ B
then, there exists atleast 1 a_{i2, j2} : a_{i2, j2} ∈ B and a_i2,j2 ∉ A
a_x,y = 1 ∀ a_x,y ∈ A
a_x,y = 1 ∀ a_x,y ∈ B

How many such (A, B) exist?

Input Format
The first line of the input contains a number N.
N lines follow, each line containing N integers (0/1) NOT separated by any space.

Output Format
Output the total number of such (A, B) pairs. If the answer is greater than or equal to 10⁹ + 7, then print answer modulo (%) 10⁹ + 7.

Constraints

2 ≤ N ≤ 1500
a_i,j ∈ [0, 1] : 0 ≤ i, j ≤ N - 1

Sample Input

4
0010
0001
1010
1110

Sample Output

10

Explanation

X means the common part of A and B.
We can swap A and B to get another answer.

0010
0001
A010
XB10

0010
0001
A010
XBB0

0010
0001
10A0
1BX0

0010
0001
10A0
BBX0

0010
0001
1010
AXB0

TimeLimits

Time limit for this challenge is mentioned here