You are given the scores of N students in three different subjects - Mathematics,*Physics* and Chemistry; all of which have been graded on a scale of 0 to 100. Your task is to compute the Pearson product-moment correlation coefficient between the scores of different pairs of subjects (Mathematics and Physics, Physics and Chemistry, Mathematics and Chemistry) based on this data. This data is based on the records of the CBSE K-12 Examination - a national school leaving examination in India, for the year 2013.

Pearson product-moment correlation coefficient

This is a measure of linear correlation described well on this Wikipedia page. The formula, in brief, is given by:

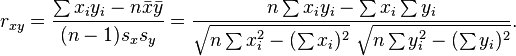
where x and y denote the two vectors between which the correlation is to be measured.

Input Format

The first row contains an integer N.
This is followed by N rows containing three tab-space ('\t') separated integers, M P C corresponding to a candidate's scores in Mathematics, Physics and Chemistry respectively.
Each row corresponds to the scores attained by a unique candidate in these three subjects.

Input Constraints

1 <= N <= 5 x 10⁵
0 <= M, P, C <= 100

Output Format

The output should contain three lines, with correlation coefficients computed
and rounded off correct to exactly 2 decimal places.
The first line should contain the correlation coefficient between Mathematics and Physics scores.
The second line should contain the correlation coefficient between Physics and Chemistry scores.
The third line should contain the correlation coefficient between Chemistry and Mathematics scores.

So, your output should look like this (these values are only for explanatory purposes):

0.12
0.13
0.95

Test Cases

There is one sample test case with scores obtained in Mathematics, Physics and Chemistry by 20 students. The hidden test case contains the scores obtained by all the candidates who appeared for the examination and took all three tests (Mathematics, Physics and Chemistry).
Think:* How can you efficiently compute the correlation coefficients within the given time constraints, while handling the scores of nearly 400k students?*

Sample Input

20
73  72  76
48  67  76
95  92  95
95  95  96
33  59  79
47  58  74
98  95  97
91  94  97
95  84  90
93  83  90
70  70  78
85  79  91
33  67  76
47  73  90
95  87  95
84  86  95
43  63  75
95  92  100
54  80  87
72  76  90

Sample Output

0.89  
0.92  
0.81

There is no special library support available for this challenge.