There are balls in a row, and each ball is either black (B) or white (W). Perform removal operations with the goal of maximizing the number of white balls picked. For each operation (where ):
- Choose an integer, , uniformly and independently from to (inclusive).
- Remove the ball from either the left end or right end of the row, which decrements the number of available balls in the row by . You can choose to remove the ball from whichever end in each step maximizing the expected total number of white balls picked at the end.
Given a string describing the initial row of balls as a sequence of W's and B's, find and print the expected number of white balls providing that you make all choices optimally. A correct answer has an absolute error of at most .
Input Format
The first line contains two space-separated integers describing the respective values of (the number of balls) and (the number of operations).
The second line describes the initial sequence balls as a single string of characters; each character is either B or W and describes a black or white ball, respectively.
Constraints
Output Format
Print a single floating-point number denoting the expected number of white balls picked. Your answer is considered to be correct if it has an absolute error of at most .
Sample Input 0
3 1
BWW
Sample Output 0
1.0000000000
Explanation 0
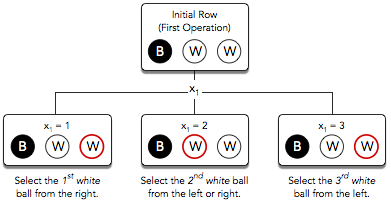
Independent of your choice of , one white ball will always be picked so the expected number of white balls chosen after operation is . Thus, we print as our answer.
Sample Input 1
4 2
WBWB
Sample Output 1
1.5000000000
Explanation 1
We perform the following operations:
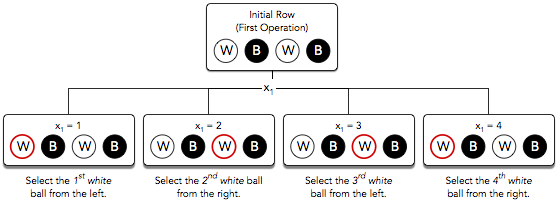
Independent of your choice of , a white ball will always be chosen during the first operation (meaning the expected number of white balls in the first operation is ).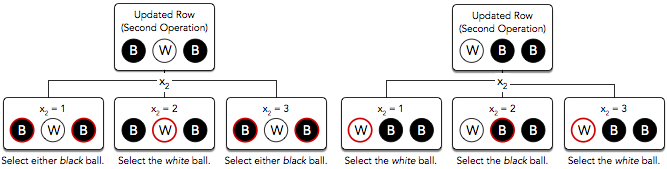
For the second operation, there are possible row orderings (depending on which ball was picked during the first operation). In the first possible row ordering, the probability of picking a white ball is . In the second possible row ordering, the probability of picking a white ball is . This means the expected number of white balls chosen in the second operation is .
After performing all operations, we print the total expected number of white balls chosen, which is .