Given an array, you are asked to perform a number of queries and divide the array into what are called, beautiful subsequences.
The array has length . A function is defined to be a minimal possible , such that it's possible to divide array into beautiful subsequences. Note that each element of an array should belong to exactly one subsequence, and subsequence does not necessarily need to be consecutive.
A subsequence with length is called beautiful if and only if:
- or
- Let be a sorted version of . It must hold that for every
For instance, if , would be . Because, you can divide into beautiful subsequences either like and or like and .
You have to answer queries. Each query is of the type:
- : you need to change a value of to , i.e. . Here is .
After each query, for the value of , lets denote that value as , where indicates the query.
You need to find modulo .
Input Format
The first line contains a single integer , representing the length of array .
The next line contains the array given as space-separated integers.
The next line contains a single integer , representing the number of queries.
Each of the lines contain two integers and , which is described above.
Constraints
Output Format
Print the required answer in one line.
Sample Input 0
5
2 2 1 1 1
2
3 2
5 5
Sample Output 0
11
Explanation 0
The initial array is
- After query the array becomes this can be divided into subsequences as , and .
- After query the array becomes this can be divided into subsequences as , , and .
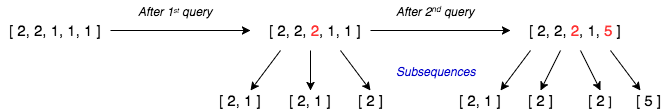
Hence, calculating we get
Sample Input 1
2
3 3
3
2 4
1 5
2 2
Sample Output 1
9
Explanation 1
The initial array is
- After query the array becomes this can be divided into subsequence as .
- After query the array becomes this can be divided into subsequence as .
- After query the array becomes this can be divided into subsequences as and .
Hence, calculating we get